1. 二叉树
特点
- 本身是有序树
- 树中各个节点的度不能超过2,即只能是0, 1 或者2.
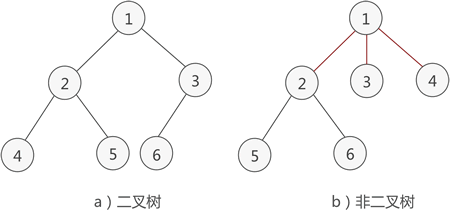
2. 满二叉树
特点
- 如果二叉树中除了叶子节点,每个节点的度都是2,则此二叉树称之为满二叉树
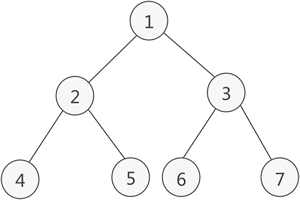
- 满二叉树除了满足普通二叉树的性质,还具有以下性质:
- 满二叉树中第 i 层的节点数为 2n-1 个。
- 深度为 k 的满二叉树必有 2k-1 个节点 ,叶子数为 2k-1。
- 满二叉树中不存在度为 1 的节点,每一个分支点中都两棵深度相同的子树,且叶子节点都在最底层。
- 具有 n 个节点的满二叉树的深度为 log2(n+1)。
3. 完全二叉树
特点
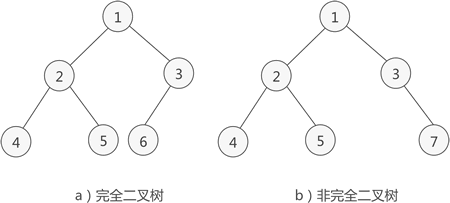
- 如果二叉树中除去最后一层节点为满二叉树,且最后一层的结点依次从左到右分布,则此二叉树被称为完全二叉树。
4. 二叉查找(搜索)树(BST树)
特点
二叉搜索树或者是一棵空树,或者是具有下列性质的二叉树:
(1)若左子树不空,则左子树上所有结点的值均小于或等于它的根节点的值;
(2)若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
(3)左、右子树也分别为二叉搜索树;
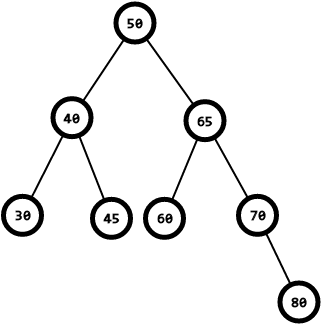
注: 二叉树性质中的有序性属于广义上的有序,包含于BST树中的特点有序.
5. 平衡二叉查找树(AVL树)
特点
- 左右子树的高度差小于等于 1。
- 其每一个子树均为平衡二叉树。
具体实现
既然引入了监督机制,我们必然需要一个监督指标,以此来判断是否需要进行平衡操作。这个监督指标被称为“平衡因子(Balance Factor)”。定义如下:
平衡因子: 某个结点的左子树的高度减去右子树的高度得到的差值。
基于平衡因子,我们就可以这样定义 AVL 树。
AVL 树: 所有结点的平衡因子的绝对值都不超过 1 的二叉树。
6.BST与AVL比较
前言
- BST树在极端的情况下查询效率为O(n),如下图,其根本原因是没能维持树的"完全形状"(像满二叉树或完全二叉树那样)
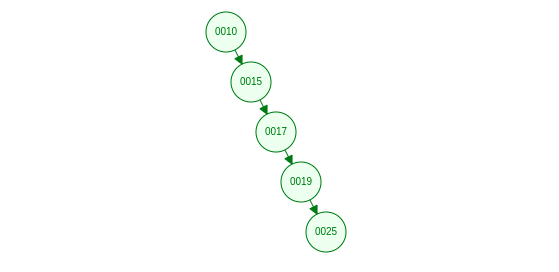
- 如果能够维持树能够像满二叉树或完全二叉树那样的结构,那么其查询效率就能打到最佳(Lg n), 同时为了保证树的"结构",需要引入"平衡因子"概念,在每一次的操作(增加, 删除, 修改)节点时, 总要保证平衡因子差的绝对值小于等于1.
7.二叉树的遍历方式
定义
- 是指从根节点出发,按照某种层序依次访问二叉树中所有节点,使得每个节点被访问一次且仅被访问依次
- 二叉树的遍历方式有很多,如果我们限制了从左到右的习惯方式,那么主要就分为四种(前序遍历, 中序遍历, 后序遍历, 层次遍历)
前序遍历
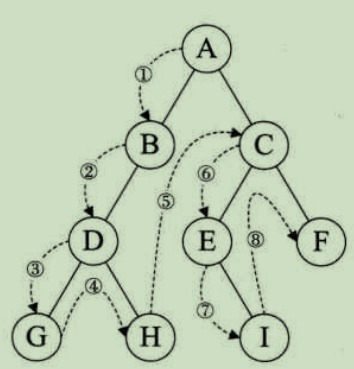
遍历结果: A B D G H C E I F
总结: 根结点 -> 左子树 -> 右子树
中序遍历
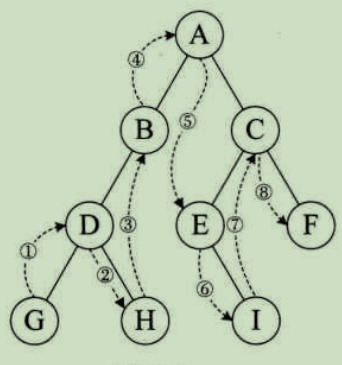
遍历结果: G D H B A E I C F
总结: 左子树 -> 根结点 -> 右子树
后序遍历
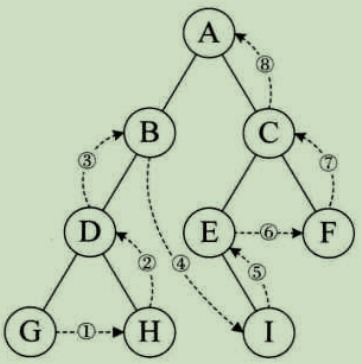
遍历结果: G H D B I E F C A
总结: 从左到右访问叶子结点 -> 根结点
层次遍历
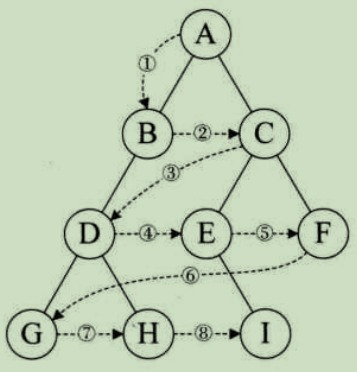
遍历结果: A B C D E F G H I
总结: 第一层 -> 第二层(从左到右访问结点)-> ··· -> 最后一层(从左到右访问结点)
二叉树遍历小结: 在BST与AVL树中,中序遍历能够保证顺序的递增,前序遍历和后序遍历中分别尾节点为最大值和首节点为最小值.
注: 深度优先遍历指的是 前序遍历, 中序遍历, 后续遍历,顾名思义深度优先是从树的深度出发去实现的遍历方式,广度优先遍历也就是从树的层次上遍历,也就是层次遍历这种方式.
8. 2-3树
定义
- 满足二分搜索树的基本性质(左子树节点值小于根节点的值, 根节点的值小于右子数的值)
- 节点可以存放一个元素或者两个元素
- 没有元素相等的节点
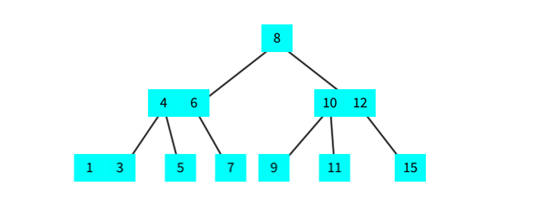
插入流程(将7,8,9.10,11,12一次插入到2-3树中流程)
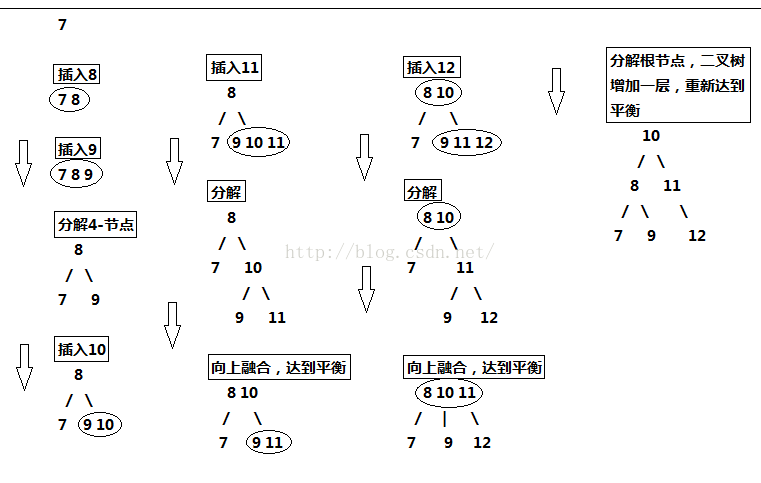
2-3树小结: 2-3树的设计完全可以保证二叉树保持矮矮胖胖的状态,保持其性能良好。但是,将这种直白的表述写成代码实现起来并不方便,因为要处理的情况太多。这样需要维护两种不同类型的节点,将链接和其他信息从一个节点复制到另一个节点,将节点从一种类型转换为另一种类型等等。
参考文档: https://zhuanlan.zhihu.com/p/104031183
